Probability And Statistics
ripetizioni di matematica online said: In mathematics, probability and statistics stand out as two significant concepts. Probability has to do with chance. Whereas, statistics is about how we handle different data using different techniques. It helps to represent complex data in a very easy and understandable way.
Statistics and probability are usually introduced in class 10, class 11 and class 12 students prepare for school exams and competitive exams.
An introduction to these essentials is given briefly in his academic books and notes.
Statistics have great applications today in data science professions. Professionals use statistics and make business forecasts. It helps them predict the future profit or loss made by the company.
What is the probability?
Probability refers to the likely outcome of any random event. The meaning of this term is to ascertain the extent to which an event is likely to occur. What is the likelihood of obtaining a head when we toss a coin into the air, for instance? The answer to this question depends on the number of possible outcomes. Here probability is either the head or tail of the outcome. So, the probability that a head will appear as a result is 1/2.
The concept of probability pertains to the assessment of the chances or probability of an event taking place. measures the certainty of an event. The probability formula is given by;
P(E) = number of positive results/number of total results
Phosphorus (E) = n (E) / n (S)
here,
n(E) = number of events favorable to event E.
n (S) = total number of visits
What is statistics?
Statistics is the study of collecting, analyzing, interpreting, presenting, and organizing data. It is a method of collecting and summarizing data. This has many applications from small to large. Whether it is the study of a country’s population or its economy, statistics are used for all of these data analyses.
Statistics encompasses a broad range of applications across numerous domains, including sociology, psychology, geology, and weather forecasting, among others.
The data collected here for analysis may be quantitative or qualitative. Quantitative data is also of two types discrete and continuous. Discrete data has a fixed value while continuous data is not a fixed data but has a range. In this concept, there exists a multitude of terminologies and formulas utilized. See the table below to understand them.

Terms used in probability and statistics
There are many terms used in the concepts of probability and statistics, such as:
- randomized Experiment
- Sample sample
- random variables
- expected value
- independence
- variance
- mean
Let us discuss these terms one by one.
Randomized Experiment
An experiment whose outcome cannot be predicted, until it is observed, is called a randomized experiment. For example, when we randomly roll a dice, the outcome is uncertain for us. We can get any output between 1 to 6. Hence, this experiment is random.
Sample space
The sample space is the set of all possible outcomes or outcomes of a random experiment. Suppose, if we roll a die at random, then the sample area for this experiment will be all possible outcomes of rolling the die, such as;
sample area = {1,2,3,4,5,6}
Random Variables
Variables that indicate possible outcomes of a random experiment are called random variables. They are of two types:
- Discrete Random Variables
- Continuous Random Variables
Discrete random variables take only those distinct values that can be counted. Whereas continuous random variables can take an infinite number of possible values.
Independent Event
When the probability of one event occurring has no effect on the probability of another event, then both events are called independent of each other. For example, if you toss a coin and simultaneously roll a die, the probability of getting a “head” is independent of the probability of getting a 6 in a die.
Mean
The mean of a random variable is the mean of the random values of the possible outcomes of a random experiment. In simple terms, it is the prediction of possible outcomes of a random experiment, which is repeated over and over or n number of times. It is also called random variable expectation.
Expected Value
The expected value is the mean of the random variable. It is the assumed value taken into account for a randomized trial. It is also called anticipation, mathematical expectation, or first moment. For example, if a six-sided die is rolled, the expected value will be the average value of all possible outcomes, i.e. 3.5.
Variance
Basically, variance tells us how the values of a random variable are spread around the mean value. Determines the sample area distribution across the medium.
List of Probability Topics
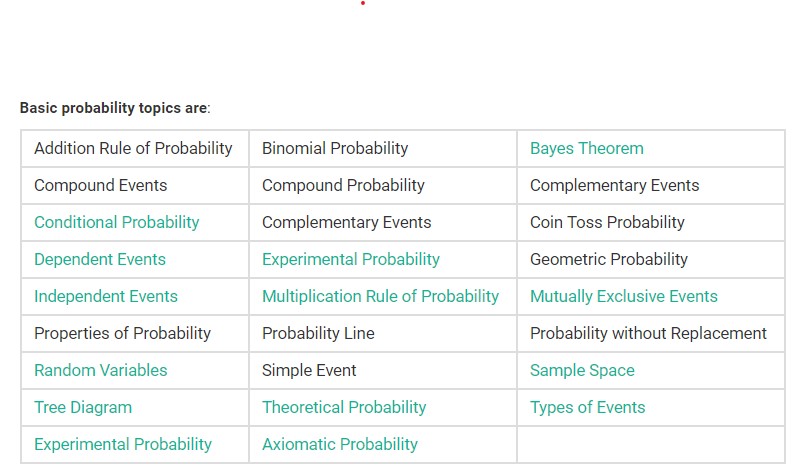
List of Statistical Topics
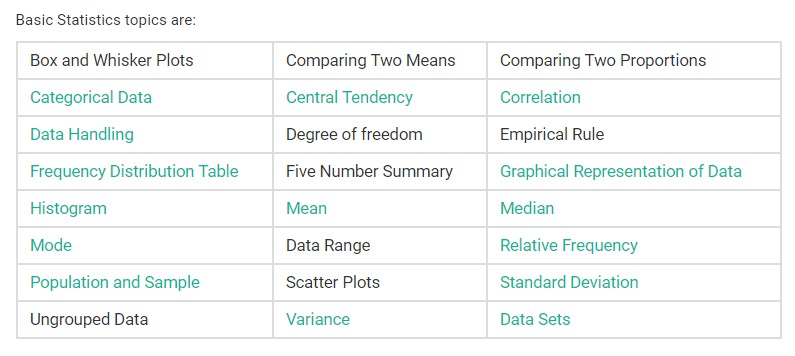
Probability and Statistics Formulas

